Logistic regression in Java with plotting

This tutorial will show how to implement an easy example of logistic regression in Java. It assumes that JavaPlot is installed. See my other tutorial (link at bottom of page) or google how to import Javaplot (it is trivial).

The major change being made here from linear regression is the hypothesis function uses the sigmoid function.

Here is the data set we will be using:

 double x1[] = {0.0, 0.5, 1.0, 1.5, 2.0, 0.1, 3.0, 3.1, 3.5, 3.2, 2.5, 2.8};   
 double x2[] = {0.0, 1.0, 1.1, 0.5, 0.3, 2.0, 3.0, 2.3, 1.5, 2.2, 3.6, 2.8};   
 double y[]  = {0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0};

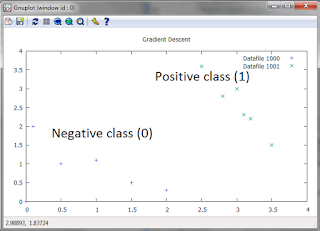
Here is a graph of the data set. We are trying to determine the boundary line, which is a line that will "split" the two groups in half.

The slight change we make will be too call the sigmoid function during gradient descent. We take the proper partial derivatives and step through m amount of examples. Here is the relevant code:

for(i = 0; i < iterations; i++)
            {
         
                h0 = 0.0;
                h1 = 0.0;
                h2 = 0.0;
               
                for(j = 0; j<m; j++)
                {
                    h0 = h0 + (sigmoid(theta0 + x1[j]*theta1 + x2[j]*theta2) - y[j]);
                    h1 = h1 + (sigmoid(theta0 + x1[j]*theta1 + x2[j]*theta2) - y[j])*x1[j];
                    h2 = h2 + (sigmoid(theta0 + x1[j]*theta1 + x2[j]*theta2) - y[j])*x2[j];
                }    
        temp0 = theta0 - (alpha*h0)/(double)m;
        temp1 = theta1 - (alpha*h1)/(double)m;
        temp2 = theta2 - (alpha*h2)/(double)m;
        theta0 = temp0;
        theta1 = temp1;
        theta2 = temp2;

}

Note that the equation we get is in two variables, x1 and x2. We will find the line by setting each to 0 and finding the intercepts. From there, we use the equation for a line to determine our boundary line. This is done in order to plot the line.

The method sigmoid(double x) is pretty straightforward. The function is rather complex but the explanation for it isn't hard to understand. See the machine learning course notes for coursera for the explanation. The code is:

private static double sigmoid(double x)
    {
        return 1 / (1 + Math.exp(-1*x));
    }
   

The resulting function is two variable as I said before. First, we need to set x2 = 0 and then x1 = 0. When those are the cases, we are left with bother theta1*x1 = theta0 and theta2*x2 = theta0. The code is as follows:

double point1 = -1 * theta0 / theta1; //x intercept

double point2 = -1 * theta0 / theta2; //y intercept

Now using these points, we can find a line using the equation for a line which is:

y - y1 = m(x-x1)

Our points are (0, point2) and (point1, 0)

Subbing in the values and isolating y we get the function for the line:

String outputFunction = String.valueOf(String.valueOf((-1*point2)/point1) + "*x+" + String.valueOf(point2));

The slope m is negative because theta0 has to be brought to the other side. Working it out on paper might make it clearer.

Here is a plot of the resulting line:

A good fit

Here is the full code. I added a plot of the cost function for the first 1000 iterations to check that it is going down. JavaPlot must be added for the plot to work. I discussed that in my post here

import com.panayotis.gnuplot.JavaPlot;
import com.panayotis.gnuplot.style.PlotStyle;
import com.panayotis.gnuplot.style.Style;

public class GradDescent {

    public static void main(String[] args) {
   
       
         double x1[] = {0.0, 0.5, 1.0, 1.5, 2.0, 0.1, 3.0, 3.1, 3.5, 3.2, 2.5, 2.8};   
         double x2[] = {0.0, 1.0, 1.1, 0.5, 0.3, 2.0, 3.0, 2.3, 1.5, 2.2, 3.6, 2.8};   
         double y[]  = {0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0};
         int counter = 0;
       
         JavaPlot p = new JavaPlot();
       
         /*number of examples*/
         int m = 12;
       
          /*thetas and temp thetas*/
            double theta0, temp0, theta1, temp1, theta2, temp2;
            theta0 = 0.0; temp0 = 0.0;
            theta1 = 0.0; temp1 = 0.0;
            theta2 = 0.0; temp2 = 0.0;
         
        /*# of iterations and learning rate*/
            int iterations = 2181800;
            float alpha = 0.009f;

            int j = 0;
            double h0 = 0.0;
            double h1 = 0.0;
            double h2 = 0.0;
           
            int i = 0;
            for(i = 0; i < iterations; i++)
            {
         
                h0 = 0.0;
                h1 = 0.0;
                h2 = 0.0;
               
                for(j = 0; j<m; j++)
                {
                    h0 = h0 + (sigmoid(theta0 + x1[j]*theta1 + x2[j]*theta2) - y[j]);
                    h1 = h1 + (sigmoid(theta0 + x1[j]*theta1 + x2[j]*theta2) - y[j])*x1[j];
                    h2 = h2 + (sigmoid(theta0 + x1[j]*theta1 + x2[j]*theta2) - y[j])*x2[j];
                }    
        temp0 = theta0 - (alpha*h0)/(double)m;
        temp1 = theta1 - (alpha*h1)/(double)m;
        temp2 = theta2 - (alpha*h2)/(double)m;
        theta0 = temp0;
        theta1 = temp1;
        theta2 = temp2;
       
        counter = counter + 1;
        if(counter < 1000)
        {
            for(j = 0; j<m; j++)
            {
                h0 = h0 + y[j]*Math.log(sigmoid(theta0 + x1[j]*theta1 + x2[j]*theta2)) + (1-y[j])*(1 - (sigmoid(theta0 + x1[j]*theta1 + x2[j]*theta2)));                                                            //+ Math.pow(( sigmoid(theta0 + x1[j]*theta1 + x2[j]*theta1) - y[j]), 2.0);
            }
            h0 = (h0 / m) * -1;
            float[][] cost = {{(float)counter, (float) h0}};
            p.addPlot(cost);
       
            System.out.println("Cost at " + counter + " is " + h0);
           
        }
       
        }
         
       p.plot();
       System.out.println(theta2 + "x2 + " + theta1 + "x1 + " + theta0);
      

    }
   
   
    private static double sigmoid(double x)
    {
        return 1 / (1 + Math.exp(-1*x));
    }
   
    private static void testGradientDescent(float n, double theta0, double theta1, double theta2)
    {
         double x3[][] = {{0.0, 0.0}, {0.5, 1.0}, {1.0, 1.1}, {1.5, 0.5}, {2.0, 0.3}, {0.1, 2.0}};   
         double x4[][] = {{3.0, 3.0}, {3.1, 2.3},{3.5, 1.5}, {3.2, 2.2}, {2.5,3.6}, {2.8, 2.8}};  
       
        JavaPlot p = new JavaPlot();
        p.set("title", "'Gradient Descent'");
        p.set("xrange", "[0:4]");
        //p.addPlot(outputFunction);
       
        p.addPlot(x3);
        p.addPlot(x4);
       
        double point1 = -1 * theta0 / theta1;
        double point2 = -1 * theta0 / theta2;
       
        String outputFunction = String.valueOf(String.valueOf((-1*point2)/point1) + "*x+" + String.valueOf(point2));
        System.out.println("Plotting " + outputFunction);
       
        PlotStyle myPlotStyle = new PlotStyle();
        myPlotStyle.setStyle(Style.LINES);
        myPlotStyle.setLineWidth(2);
       
        double boundaryLine[][] = {{point1, 0},{0, point2}};
        //p.addPlot(boundaryLine);
        p.addPlot(outputFunction);
        p.plot();
       
    }

}